While accurate sulcal identification can be a challenge even for expert neuroanatomists, there are sulci that are to some degree more consistent, and for which anatomical correspondence can be established across subjects. These are the larger primary sulci. The localization of these sulci allows us to generate a spatial distribution or probabilistic map which can be used to label candidate sulci. A graph that maps the structural relationships between sulci can also be constructed and unlabeled sulci (or the more variable secondary and tertiary sulci) can be identified against this reference.
These two ideas, the use of the probabilistic atlas and the graph, have been incorporated into automated and semi-automated labeling methods in various ways. In this post I will present the basic idea behind the use of the spatial distribution model.
The use of a probabilistic atlas
Probabilistic maps compute the probability for each tissue class at every voxel location using a large database of segmented and labeled anatomical structures. Evans et al. [3] coined the name Statistical Probabilistic Anatomical Maps or SPAM for these models. Paul Thompson has a nice description of these SPAM models and the Brainvisa website has a nice visualization of a sulcal atlas which is reproduced below:
A straightforward implementation of the probabilistic atlas paradigm can be seen in Le Goualher et al. [1] [2]. SPAM models give the probability for each sulcal class so that at any given location, unlabeled sulci are assigned the most probable label for that location. In other words, to label a new sulcus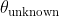 :
:
Compute:![\theta_k = \arg\max_{\theta}[p(\theta_i)]](http://latex.codecogs.com/gif.latex?\theta_k = \arg\max_{\theta}[p(\theta_i)]) where p is the probability from a SPAM atlas
where p is the probability from a SPAM atlas
Assign: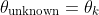
The use of a point distribution model
A different spatial distribution model is used by Lohmann et al. [4]. A point distribution model introduced by Cootes et al. [5] computes the shape of sulcal basins across a training set. Any unlabeled sulcus can be expressed as a linear combination of the eigenvalues generated from the PCA of this shape covariance matrix; an optimization over the linear function gives the best label.
Spatial distribution models give spatial bounds but this is not adequate to discriminate between the sulci in a local region. They are usually combined with graphs which model connections between sulci thus giving local structural context. In the combined strategy, the spatial information is used to supply spatial priors [6], localization constraints or to narrow the search space in an optimization or graph matching process [7].
I will write about the use of graph models in my next post.
References
1) Georges Le Goualher, D. Louis Collins and Christian Barillot, Alan C. Evans, "Automatic Identification of Cortical Sulci Using a 3D Probabilistic Atlas," In MICCAI, 1998, pp. 509-518.
2) Georges Le Goualher, E. Procyk, D.L. Collins, R. Venugopal, Christian Barillot, "Automated Extraction and Variability Analysis of Sulcal Neuroanatomy," IEEE Trans. Med. Imag., 18(3), 1999, pp. 206-217.
3) A. C. Evans, D. L. Collins, P. Neelin, M. Kamber, S. Marrett, "Three-dimensional correlative imaging: Applications in human brain mapping," Advances in Functional NeuroImaging: Technical Foundations,(ed. R. Thatcher and M. Hallett and T. Zeffiro and E. John and M. Huerta) Academic Press, 1994, pp. 145-162.
4) Gabrielle Lohmann and Y. von Cramon, "Automatic labeling of the human cortical surface using sulcal basins," IEEE Trans. Med. Imag., 4, 2000, pp. 179-188.
5) Timothy F. Cootes, Christopher J. Taylor, David H. Cooper, Jim Graham, "Active Shape Models-Their Training and Application," Computer Vision and Image Understanding, 61(1), 1995, pp. 38-59.These two ideas, the use of the probabilistic atlas and the graph, have been incorporated into automated and semi-automated labeling methods in various ways. In this post I will present the basic idea behind the use of the spatial distribution model.
The use of a probabilistic atlas
Probabilistic maps compute the probability for each tissue class at every voxel location using a large database of segmented and labeled anatomical structures. Evans et al. [3] coined the name Statistical Probabilistic Anatomical Maps or SPAM for these models. Paul Thompson has a nice description of these SPAM models and the Brainvisa website has a nice visualization of a sulcal atlas which is reproduced below:
A straightforward implementation of the probabilistic atlas paradigm can be seen in Le Goualher et al. [1] [2]. SPAM models give the probability for each sulcal class so that at any given location, unlabeled sulci are assigned the most probable label for that location. In other words, to label a new sulcus
Compute:
Assign:
The use of a point distribution model
A different spatial distribution model is used by Lohmann et al. [4]. A point distribution model introduced by Cootes et al. [5] computes the shape of sulcal basins across a training set. Any unlabeled sulcus can be expressed as a linear combination of the eigenvalues generated from the PCA of this shape covariance matrix; an optimization over the linear function gives the best label.
Spatial distribution models give spatial bounds but this is not adequate to discriminate between the sulci in a local region. They are usually combined with graphs which model connections between sulci thus giving local structural context. In the combined strategy, the spatial information is used to supply spatial priors [6], localization constraints or to narrow the search space in an optimization or graph matching process [7].
I will write about the use of graph models in my next post.
References
1) Georges Le Goualher, D. Louis Collins and Christian Barillot, Alan C. Evans, "Automatic Identification of Cortical Sulci Using a 3D Probabilistic Atlas," In MICCAI, 1998, pp. 509-518.
2) Georges Le Goualher, E. Procyk, D.L. Collins, R. Venugopal, Christian Barillot, "Automated Extraction and Variability Analysis of Sulcal Neuroanatomy," IEEE Trans. Med. Imag., 18(3), 1999, pp. 206-217.
3) A. C. Evans, D. L. Collins, P. Neelin, M. Kamber, S. Marrett, "Three-dimensional correlative imaging: Applications in human brain mapping," Advances in Functional NeuroImaging: Technical Foundations,(ed. R. Thatcher and M. Hallett and T. Zeffiro and E. John and M. Huerta) Academic Press, 1994, pp. 145-162.
4) Gabrielle Lohmann and Y. von Cramon, "Automatic labeling of the human cortical surface using sulcal basins," IEEE Trans. Med. Imag., 4, 2000, pp. 179-188.
6) M. Perrot, D. Rivière, J.-F. Mangin, "Identifying cortical sulci from localizations, shape and local organization," ISBI, 2008, pp. 420-423.
7) Yang, F & Kruggel, F., "A graph matching approach for labeling brain sulci using location, orientation, and shape," Neurocomputing, 2009, pp. 179-190.
Posts on Sulcal Labeling
1) Why we label sulci
2) Why is sulcal labeling difficult ?
3) The use of a spatial distribution model in labeling sulci


