Artful artichokes, showy 'shrooms,
seeds cantilevered in cantaloupe.
Fractal flows,
and more
at this MRI show.
Tuesday, July 27, 2010
Saturday, July 24, 2010
To find a mean in a nonlinear manifold
These are some notes on the Karcher mean. I will be updating this post hopefully in the coming weeks.
In a Euclidean space, for a set of k points, x_1, x_2 ... x_k, the sample mean is: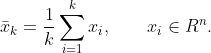
In a nonlinear manifold, a simple summation is no longer possible. We can, however, make an extrinsic computation by embedding the manifold in a vector space, computing the Euclidean mean and projecting the result back into the manifold. A disadvantage of this approach is that the mean computed depends on the choice of embedding.
A second possibility is an intrinsic computation, i.e., one where we use intrinsic manifold computations to compute the mean.
To compute an intrinsic mean within a manifold, M, we use the concept of the mean as the centroid of a density. This idea was put forward by Fréchet to calculate means in a Riemanniann manifold. The computation involved a minimization but the existence and uniqueness of the resulting mean could not be guaranteed (see Pennec's 1999 NSIP paper for details). Karcher's proposal that a local instead of a global mean be used (see Karcher's 1977 paper), led to a practical implementation. We shall henceforth refer to this local mean as the Karcher Mean.
(To be updated ...)
Karcher Mean references I found helpful
Ricardo Ferreira et al. have a paper entitled Newton Method for Riemannian centroid computation in naturally reductive homogeneous spaces which has implementation details such as the intrinsic manifold computations for well known manifolds such as the sphere, the special orthogonal group, SO(n), and the space of positive definite matrices.
Bibliography
1) M. Fréchet, "Les elements aléatoires de nature quelconque dans un espace
distancié," Annales de l'Institut Henri Poincaré, Vol. 10, (1948) pp. 215-310.
2) X. Pennec, “Probabilities and statistics on Riemannian manifolds: Basic tools for geometric measurements,” in Proc. NSIP'99, Vol. 1, (1999), pp. 194–198.
3) H. Karcher, Riemannian center of mass and mollifier smoothing. Commun. Pure and Appl. Math. 30 (1977), pp. 509–541.
In a Euclidean space, for a set of k points, x_1, x_2 ... x_k, the sample mean is:
In a nonlinear manifold, a simple summation is no longer possible. We can, however, make an extrinsic computation by embedding the manifold in a vector space, computing the Euclidean mean and projecting the result back into the manifold. A disadvantage of this approach is that the mean computed depends on the choice of embedding.
A second possibility is an intrinsic computation, i.e., one where we use intrinsic manifold computations to compute the mean.
To compute an intrinsic mean within a manifold, M, we use the concept of the mean as the centroid of a density. This idea was put forward by Fréchet to calculate means in a Riemanniann manifold. The computation involved a minimization but the existence and uniqueness of the resulting mean could not be guaranteed (see Pennec's 1999 NSIP paper for details). Karcher's proposal that a local instead of a global mean be used (see Karcher's 1977 paper), led to a practical implementation. We shall henceforth refer to this local mean as the Karcher Mean.
(To be updated ...)
Karcher Mean references I found helpful
Ricardo Ferreira et al. have a paper entitled Newton Method for Riemannian centroid computation in naturally reductive homogeneous spaces which has implementation details such as the intrinsic manifold computations for well known manifolds such as the sphere, the special orthogonal group, SO(n), and the space of positive definite matrices.
Bibliography
1) M. Fréchet, "Les elements aléatoires de nature quelconque dans un espace
distancié," Annales de l'Institut Henri Poincaré, Vol. 10, (1948) pp. 215-310.
2) X. Pennec, “Probabilities and statistics on Riemannian manifolds: Basic tools for geometric measurements,” in Proc. NSIP'99, Vol. 1, (1999), pp. 194–198.
3) H. Karcher, Riemannian center of mass and mollifier smoothing. Commun. Pure and Appl. Math. 30 (1977), pp. 509–541.
Thursday, July 1, 2010
The corpus callosum and interhemispheric communication
The corpus callosum (CC), with over 300 million fibers, is the largest white matter fiber bundle in the human brain. (It is easily identifiable in conventional MRI scans.) Topographically, it is centered along the midsagittal plane with radiations that extend to the prefrontal and frontal cortex in the anterior brain, the sensory-motor cortex in the middle and the parietal, temporal and occipital lobes in the posterior half of the brain.
This large and heterogeneous collection of fibers is responsible for interhemispheric communication. Michael Gazzaniga, a neuroscientist at Dartmouth College, has being studying the nature of this left brain- right brain communication for over 30 years. Here he explains some of his fascinating findings to Alan Alda, former hawkeye, now host of Scientific American Frontiers. And this is one of Gazzaniga's papers. (A similar account of the mysterious workings of the brain first got me interested in brain imaging. The book in question was V.S. Ramachandran's Phantoms in the Brain.)
Because of the important role it plays, the CC is the focus of many studies. Some are concerned with changes in the shape, size or structure of the CC. These changes may occur due to aging or degenerative disease. On one end of the spectrum, work is being done to provide tools to measure and monitor these changes. At the other end are the clinical studies. An example of a clinical study might be one that links the different stages of the disease or aging process with physical alterations.
This large and heterogeneous collection of fibers is responsible for interhemispheric communication. Michael Gazzaniga, a neuroscientist at Dartmouth College, has being studying the nature of this left brain- right brain communication for over 30 years. Here he explains some of his fascinating findings to Alan Alda, former hawkeye, now host of Scientific American Frontiers. And this is one of Gazzaniga's papers. (A similar account of the mysterious workings of the brain first got me interested in brain imaging. The book in question was V.S. Ramachandran's Phantoms in the Brain.)
Because of the important role it plays, the CC is the focus of many studies. Some are concerned with changes in the shape, size or structure of the CC. These changes may occur due to aging or degenerative disease. On one end of the spectrum, work is being done to provide tools to measure and monitor these changes. At the other end are the clinical studies. An example of a clinical study might be one that links the different stages of the disease or aging process with physical alterations.
Subscribe to:
Posts (Atom)